Колегаева Елена Михайловна, доцент кафедры математических методов и информационных технологий ДВАГС
I. Преобразование иррациональных выражений.
Рррациональным называется выражение, содержащее РєРѕСЂРЅРё n-РѕР№ степени.
1) Одно из типичных преобразований иррациональных выражений – избавление от иррациональности в знаменателе.
а) Если в знаменателе стоит выражение вида  , то необходимо числитель и знаменатель умножить на сопряженное к нему выражение
, то необходимо числитель и знаменатель умножить на сопряженное к нему выражение 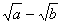 . В этом случае применяется формула
. В этом случае применяется формула  .
.
б) Если в знаменателе стоит выражение   (или
 (или  ), то числитель и знаменатель умножается, соответственно, на
), то числитель и знаменатель умножается, соответственно, на   (или
 (или  ). В этом случае применяются формулы
). В этом случае применяются формулы
 ,
,
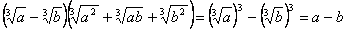 .
.
Пример 1. Рзбавиться РѕС‚ иррациональности РІ знаменателе:
Р°)  ;В В В В Р±)
;В В В В Р±)  ;В В В В РІ)
;В В В В РІ)  ;В В В В Рі)
;В В В В Рі)  ; Рґ)
; Рґ)  ;В В В В Рµ)
;В В В В Рµ)  .
.
Решение:
Р°)  ;
;
Р±)  ;
;
РІ)  ;
;
Рі)  ;
;
Рґ) 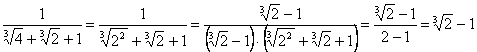 ;
;
Рµ) 
 .
.
Отметим еще одно свойство:

которое часто применяется в преобразованиях.
Пример 2. Упростить выражение:
Р°)  ;В В В В Р±)
;В В В В Р±)  ;В В В В РІ)
;В В В В РІ)  .
.
Решение:
Р°) 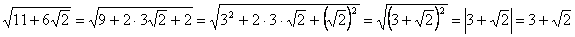 , С‚.Рє.
, С‚.Рє.  .
.
Р±)  , С‚.Рє.
, С‚.Рє. 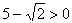 .
.
РІ) 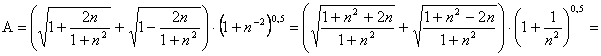
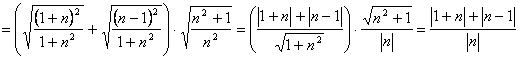 .
.
Выясним, при каких n выражения под знаком модуля меняют знак: n=-1, n=1, n=0. 1) Если n

2) Если -1Јn
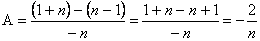
3) Если 0

4) Если nі1, то
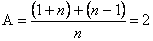
Ответ: 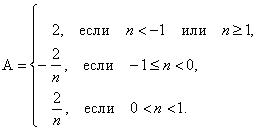
II. Рррациональные уравнения.
Рассмотрим уравнение вида 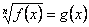 .
.
Основной метод решения – возведение обеих частей уравнения в степень n. При этом, если n – четное, то могут возникнуть посторонние корни. Поэтому в уравнениях необходимо делать проверку.
Если уравнение содержит два и больше корней, то один из корней «уединяется», то есть уравнение приводится к виду  .
.
Еще один способ решения – введение вспомогательной переменной.
Пример 3. Решить уравнения:
Р°)  ;
;
Р±)  ;
;
РІ)  ;
;
Рі)  .
.
Решение:
Р°)     Ы В
   Ы   ;
;



Проверка.
 В
 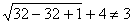  Ю х=-4 – посторонний корень,
 Ю х=-4 – посторонний корень,
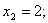 В
 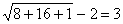  – верно Ю х=2 – корень.
 – верно Ю х=2 – корень.
Ответ: х=2.
Р±) 




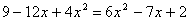


Проверка.
 В
 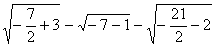   –  это выражение не существует, т.е.
  –  это выражение не существует, т.е.
  – посторонний корень,
 – посторонний корень,
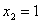 В
   – верно Ю
 – верно Ю   – корень.
 – корень.
Ответ:  .
.
РІ) 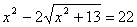
Введем вспомогательную переменную   Ю x2=t2–13
 Ю x2=t2–13
t2-13-2t=22; t2-2t-35=0,
t1=7; t2=-5.
Сделаем обратную замену:
 В Р« С…2+13=49 Р« С…2=36 Р® С…=В±6,
В Р« С…2+13=49 Р« С…2=36 Р® С…=В±6,
  – не имеет решений.
 – не имеет решений.
Ответ: х=±6.
Рі) 
Сделаем замену переменной. Положим  . Тогда уравнение примет вид:
. Тогда уравнение примет вид:
 В Р«
В Р«  В Р«
В Р« 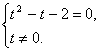

 В Р®
В Р® 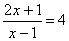 В Р«
В Р«  В Р«
В Р« 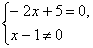 В Р«
В Р« 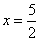 .
.
Проверка показывает, что   – корень.
 – корень.
Ответ:  .
.
III. Решение иррациональных неравенств.
При решении этих неравенств следует помнить, что в четную степень можно возводить неравенства с неотрицательными членами.
Поэтому неравенство   эквивалентно системам
 эквивалентно системам
  или
 или 
Неравенство   равносильно системе
 равносильно системе

Пример 4. Решить неравенства:
Р°)  В Р±)
В Р±) 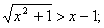
РІ)  В Рі)
В Рі) 
Решение.
Р°)  В Р«
В Р«  В Р«
В Р« 
Решим третье неравенство системы методом интервалов:
x2-5x-14>0
x2-5x-14=0


(x-7)(x+2)>0

Найдем пересечение решений трех неравенств: Ответ: -18Јx
Р±) 
если х-1Ј0, то неравенство верно, то есть хЈ1;
если x-1>0 Рё так как x2+1>0, РІРѕР·РІРѕРґРёРј РѕР±Рµ части РІ квадрат. Рмеем:
 В Р«
В Р« 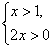 В Р« x>1.
В Р« x>1.
Объединяем два решения, получим х – любое.
Ответ: х – любое.
РІ) 
 В Р«
В Р«  В Р«
В Р«  В Р«
В Р«
 В Р«
В Р«  В Р«
В Р«

Ответ: хі1.
Рі) 

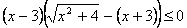
  илиВ
 или 
 В
В 
 В
В 
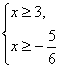 В Р« С…С–3
В Р« С…С–3 
 В
В  В
В 
Ответ:  .
.
Задачи для самостоятельного решения
Уважаемые ребята, ниже приводятся задания для самостоятельного решения, которые следует выполнить, оформить отдельно от заданий по другим предметам и выслать в адрес Хабаровской краевой заочной физико-математической школы.
Наш адрес: 680000, г. Хабаровск, ул. Дзержинского, 48, ХКЦТТ ( ХКЗФМШ).
М11.9.1. Упростить:
1)  В 2)
В 2) 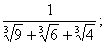 В 3)
В 3) 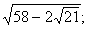
4)  , если
, если  , m>0, 0
, m>0, 0
М11.9.2. Решить уравнения
 ;
;
 ;
;
 ;
;
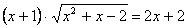 .
.
М11.9.3. Решить неравенства:
 ;
;
 ;
;
 ;
;
 .
.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.khspu.ru



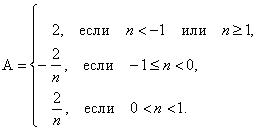

 В Р«
В Р« 
 В Р«
В Р«
 В
В 