Экспериментальное исследование взаимодействия упругих волн в акустическом резонаторе.

В.Е.Назаров, А.В.Радостин, И.А.Соустова, Институт прикладной физики РАН

В акустике подробно изучены нелинейные эффекты, возникающие при распространении и взаимодействии упругих волн в твердых телах, уравнение состояния которых описываются 5-ти константной теорией упругости. Подобный подход, как правило, справедлив для описания однородных сред. Для микронеоднородных сред, в частности горных пород, содержащих различные дефекты (дислокации, зерна, трещины и т.д.) даже при относительно небольших деформациях, уравнение состояния часто характеризуется неоднозначной (гистерезисной) зависимостью «напряжение – деформация» и может также содержать диссипативную нелинейность. При распространении интенсивных упругих волн в таких средах наблюдаются нелинейные эффекты: амплитудно-зависимые потери, изменение скорости волны, генерация высших гармоник и т.д. Наиболее сильно эти эффекты проявляются в акустических резонаторах. Такие эксперименты проводились с некоторыми металлами и горными породами [1-3]. В настоящей работе представлены результаты экспериментальных исследований влияния мощной волны накачки на слабую волну в резонаторе из песчаника - горной породы, встречающейся в местах добычи нефти и газа. Эксперименты проводились со стержневым резонатором диаметром d = 2.5см и длиной L = 28см. Блок-схема измерительной установки представлена рис.2.

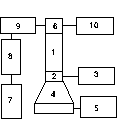
Р РёСЃ.2

Р РёСЃ.3

Пьезокерамический излучатель слабой волны (2) был приклеен к торцу образца (1) и массивному (М= 2 кг) титановому концентратору (4), являющемуся излучателем мощной волны накачки (ее минимальный уровень превышал максимальный уровень слабой волны примерно на 30 дБ), так что граничное условие на этом торце резонатора было близко к условию на абсолютно жесткой поверхности. К другому концу стержня приклеивался пьезоакселерометр (6) достаточно малой массы, так что эта граница была близка к акустически мягкой. Для таких резонаторов спектр собственных частот определяется следующим выражением: fn=c0(2n-1)/4L, где c0 - скорость продольной волны в стержне, n = 1,2…- номер продольной моды резонатора. С пьезоакселерометра сигнал поступал на спектроанализатор (10) для измерения амплитуды накачки, а также через режекторный фильтр (9), подавляющий сигнал на частоте накачки на 30 дБ, на селективный вольтметр (8) и осциллограф (7), где производилось измерение уровня слабого сигнала. Собственные частоты первых продольных мод резонатора при малых амплитудах возбуждения составляли соответственно 2250 Гц, 6800 Гц, 10150 Гц и 16650 Гц, а добротности - 45, 90, 81 и 93. Таким собственным частотам соответствует c0»2500 м/с. Измерения проводились для слабой волны на 4-й моде резонатора и для накачки на 1-й моде, а также - наоборот. На рис.3 приведены резонансные кривые для слабой волны на 4-й моде в присутствии накачки на 1-й моде при различных ее амплитудах. Видно, что с ростом амплитуды волны накачки происходит сдвиг резонансной частоты и расширение резонансной кривой, т.е. уменьшение добротности резонатора

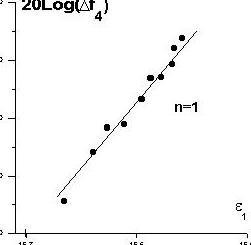
Р РёСЃ.4

Р РёСЃ.5

На рис.4 в логарифмическом масштабе приведена зависимость сдвига резонансной частоты DF от амплитуды деформации волны накачки e1, из которого следует, что DF µe1. На рис.5 приведена зависимость амплитуды слабой волны A (в резонансе) от e1, из которого видно, что A µe1. Аналогичные зависимости наблюдались и в случае возбуждения слабой волны на 1-й моде резонатора, а накачки - на 4-й.

Аналитическое описание сдвига резонансной частоты проведено в рамках уравнения состояния, содержащего упругую нелинейность:

,

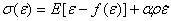где E- модуль Юнга, f(e) - малая нелинейная поправка (|f(e)|

,

где A0- амплитуда слабой волны, создаваемой излучателем, d=wn-w - расстройка частоты от резонанса, B0==ge1, где g - эффективный параметр упругой нелинейности песчаника. Из сравнения экспериментальной и аналитической зависимости получаем оценку для параметра упругой нелинейности песчаника: g »2Ч103. Отметим, что полученное значение параметра упругой нелинейности существенно превышает характерные значения для однородных сред (g

Таким образом, уравнение состояния, содержащее упругую нелинейность, описывает только сдвиг резонансной частоты, и не описывает уменьшение добротности резонатора для слабой волны в поле мощной волны накачки. Для объяснения этого эффекта необходимо предположить, что песчаник обладает также и диссипативной акустической нелинейностью.

Работа выполнена при поддержке РФФИ (гранд 96-15-96603).

Список литературы

 «Три взгляда на акустику помещений» А.П. Ефимов, журнал «Install Pro Magazine», 2000 г.

Назаров В.Е., Островский Л.А., Соустова И.А., Сутин А.М. «Акустический журнал», №3,1988 г.

«Физика металлов и металловедение» Назаров В.Е. 1992.

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://www.referat.ru