Предварительная
обработка оцифрованного изображения объекта включает выделение, сглаживание и
векторизацию контура. Под векторизацией будем понимать процесс сопоставления
контуру последовательности конечномерных векторов, характеризующих изображение
объекта. Все способы векторизации можно разделить на векторизацию по контрольным
точкам и пошаговую векторизацию. К последним относится широкий класс методов,
использующих так называемое преобразование Хау (см. [1], [2]). В качестве контрольных
точек могут быть угловые точки [3], точки экстремума функции кривизны [4],
точки перегиба и др.
В статье рассмотрен
простой алгоритм выделения контрольных точек и построения инвариантного
векторного представления изображения объекта. Кроме того, предложен способ
функционализации векторного представления изображения. Результатом функционализации
является некоторая функция изображения, по которой частично или полностью может
быть восстановлено векторное представление. В ряде задач, например, при распознавании
симметрий, анализ функции изображения позволяет получить дополнительную информацию
об изображении. Обсуждаются вопросы устойчивости функции изображения к
изменению центра масс векторного представления, к появлению новой контрольной
точки и т.д.
2.
Алгоритм прослеживания контура и выявления контрольных точек
Рассмотрим дискретное
бинарное изображение   на фоне
 на фоне 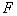 . Считаем, что
. Считаем, что 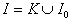 , где
, где 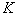  - контур изображения,
 - контур изображения, 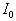  - внутренность
изображения
 - внутренность
изображения  ,
, 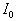  - может, в частности,
содержать другие контуры. Кроме того, считаем, что изображение
 - может, в частности,
содержать другие контуры. Кроме того, считаем, что изображение 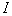  является сглаженным и
не содержит висячих точек. Введем матрицу
 является сглаженным и
РЅРµ содержит висячих точек. Введем матрицу 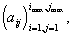 В
 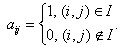  Будем рассматривать
следующие параметры:
 Будем рассматривать
следующие параметры: 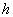 ,
, 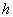
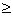 0, - начальный порог отбора контрольных точек;
0, - начальный порог отбора контрольных точек; 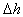 ,
, 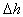 >0 - изменение порога отбора контрольных точек;
>0 - изменение порога отбора контрольных точек; 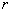 ,
, 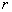 >0 - размер окрестности контрольной точки. Нам потребуется
вычислять расстояние между элементами, задающими изображение и фон, т.е.
необходимо ввести некоторую метрику
>0 - размер окрестности контрольной точки. Нам потребуется
вычислять расстояние между элементами, задающими изображение и фон, т.е.
необходимо ввести некоторую метрику 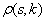  на дискретной плоскости.
В качестве метрики
 на дискретной плоскости.
В качестве метрики 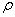  можно использовать
 можно использовать  ,
,  ,
, 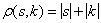  и др. Алгоритм,
позволяющий проследить контур изображения и сформировать массив контрольных
точек, состоит из следующих шагов.
 и др. Алгоритм,
позволяющий проследить контур изображения и сформировать массив контрольных
точек, состоит из следующих шагов.
 Просматриваем элементы матрицы   слева - направо,
сверху - вниз и находим первый элемент
 слева - направо,
сверху - вниз и находим первый элемент 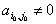 . Полагаем
. Полагаем 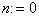 ,
,
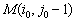 . Здесь
. Здесь   - номер отслеживаемой
точки контура;
 - номер отслеживаемой
точки контура; 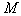  - точка начала обхода
вокруг последней отслеживаемой точки контура с целью отслеживания текущей
точки.
 - точка начала обхода
вокруг последней отслеживаемой точки контура с целью отслеживания текущей
точки.
 Рассмотрим  -окрестность точки
-окрестность точки 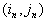 В
В 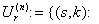 В
 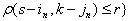 . Подсчитаем количество точек
. Подсчитаем количество точек 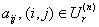 , принадлежащих фону
, принадлежащих фону 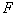  и не принадлежащих
ему:
 и не принадлежащих
ему: 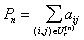 ,
, 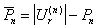 , РіРґРµ
, где   - мощность (количество
точек) окрестности
 - мощность (количество
точек) окрестности 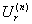 .
.
 Вычисляем вес 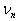 В
  -й точки:
-й точки:    .
В В .
 Если 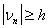 , то
, то 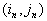  - контрольная точка. В
этом случае добавляем
 - контрольная точка. В
этом случае добавляем 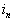  в вектор
 в вектор  ,
,   - в вектор
 - в вектор 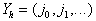 ,
, 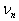  - в вектор
 - в вектор  .
.
 Продолжаем обход контура. Пусть 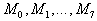  - элементы матрицы
 - элементы матрицы 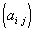 , расположенные вокруг элемента
, расположенные вокруг элемента   по часовой стрелке,
причем
 по часовой стрелке,
причем 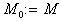 . Осуществляем поиск первого ненулевого матричного элемента
из окружающих его элементов
. Осуществляем поиск первого ненулевого матричного элемента
из окружающих его элементов 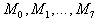 . Если
. Если 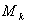 такой элемент, то полагаем
такой элемент, то полагаем   и
В Рё  .
.
 Если 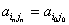 , то обход контура изображения окончен и переходим к пункту 80.,
в противном случае - к пункту 30.
, то обход контура изображения окончен и переходим к пункту 80.,
в противном случае - к пункту 30.
 Пусть   - длина вектора
 - длина вектора 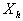  (число контрольных
точек). Если
 (число контрольных
точек). Если   (т.е. число
контрольных точек невелико), то
 (т.е. число
контрольных точек невелико), то 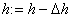  и переходим к пункту 10(осуществляем новый обход контура). Если
 и переходим к пункту 10(осуществляем новый обход контура). Если  , то массив контрольных точек построен.
, то массив контрольных точек построен.
Данный алгоритм был
реализован и апробирован в системе Borland Delphi.
РќР° СЂРёСЃ. 1 Рё 2
представлены результаты векторизации бинарного изображения. Результаты работы
программы сведены в таблицу 1.
Очевидно, что в
контрольных точках граница изображения претерпевает наиболее существенные изломы.
Поэтому многоугольник 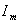 , полученный путем последовательного соединения контрольных
точек отрезками прямых линий, является аппроксимацией исходного изображения.
При этом чем больше число контрольных точек, тем точнее аппроксимация. В
качестве оценки относительной погрешности такого представления изображения
можно использовать величину
, полученный путем последовательного соединения контрольных
точек отрезками прямых линий, является аппроксимацией исходного изображения.
При этом чем больше число контрольных точек, тем точнее аппроксимация. В
качестве оценки относительной погрешности такого представления изображения
можно использовать величину 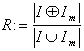 ,
,
РіРґРµ 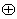 В - СЃРёРјРІРѕР»
симметрической разности множеств.
В - СЃРёРјРІРѕР»
симметрической разности множеств.
В  В В В В В В В В В В В В В В В В В В
В В В В В В В В В В В В В В В В В В 
В В В В В В В В В В В В В В В В В В Р РёСЃ. 1В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
Р РёСЃ. 2
Табл. 1
|
|
Окрестность
|
Число контрольных точек
|
Весовой порог
|
R
|
|
Р РёСЃСѓРЅРѕРє 1
|
Квадрат 5*5
|
6
|
0.56
|
16.55%
|
|
Р РёСЃСѓРЅРѕРє 2
|
Квадрат 5*5
|
14
|
0.52
|
1.38%
|
На рис. 3 приведены
графики изменения числа контрольных точек и их прироста в зависимости от выбранного
РїРѕСЂРѕРіР° h.

Р РёСЃ. 3.
Прирост точек
количественно равен уменьшению числа контрольных точек при увеличениях весового
порога. Оптимальное пороговое значение следует выбирать из интервала от (h?, h??), где h? - значение весового порога, соответствующее
максимуму прироста числа контрольных точек, h- значение, начиная с
которого число контрольных точек равно нулю. Следует отметить, что в литературе
имеется указание на то, что оптимальным для распознавания изображений считается
получение приблизительно 40 контрольных точек [4].
3.
Формирование векторного представления контура
После выполнения
алгоритма прослеживания контура и выявления контрольных точек имеется три
вектора: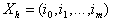 ,
,  ,В
,   - абсциссы, ординаты и
веса контрольных точек соответственно. Тройку
 - абсциссы, ординаты и
веса контрольных точек соответственно. Тройку 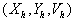  назовем скелетом
изображения
 назовем скелетом
изображения  . Далее вычислим:
. Далее вычислим:
центр масс контрольных
точек  , где
, РіРґРµ 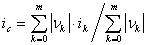 ,
, 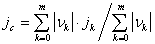 ;
;
длины радиус-векторов
контрольных точек относительно центра масс:  ,
,  , а также длины нормированных радиус-векторов
, а также длины нормированных радиус-векторов 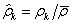 , где
, РіРґРµ  ;
;
косинусы углов между
соседними радиус-векторами контрольных точек: 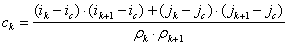 ,
,   ( считая
 ( считая 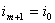 ,
, 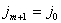 В )
В )
РР· вычисленных компонент
составляем векторы  В
  . Векторы
. Векторы 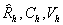  будут инвариантны
относительно сдвига, поворота и гомотетии изображения относительно центра масс
(если «замкнуть» эти векторы, считая
 будут инвариантны
относительно сдвига, поворота и гомотетии изображения относительно центра масс
(если «замкнуть» эти векторы, считая  ). Четверку
). Четверку 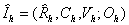  будем называть
нормированным векторным представлением изображения
 будем называть
нормированным векторным представлением изображения 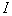 . Рассмотрим вопрос об устойчивости центра масс изображения к
добавлению новой контрольной точки.
. Рассмотрим вопрос об устойчивости центра масс изображения к
добавлению новой контрольной точки.
Теорема 1. Если к
нормированному векторному представлению 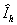  добавить контрольную
точку
 добавить контрольную
точку 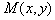 с весом
с весом 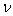 , то для евклидова расстояния между новым центром тяжести
, то для евклидова расстояния между новым центром тяжести 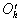  и старым
 и старым 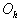  справедлива оценка
 справедлива оценка 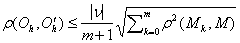 , где
, где 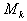 - точки скелета изображения
- точки скелета изображения  . В частности, если
. В частности, если 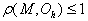 , то
, то 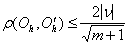 .
.
Другими словами, если
число контрольных точек достаточно велико, а вес новой точки небольшой, то
центр симметрии сместится незначительно.
4.Функция
изображения
Вместо анализа
векторного представления 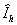  в ряде задач (одна из
которых будет рассмотрена в следующем разделе) удобней изучать свойства
некоторой функции, связывающей векторы из представления
 в ряде задач (одна из
которых будет рассмотрена в следующем разделе) удобней изучать свойства
некоторой функции, связывающей векторы из представления  . Например, рассмотрим функцию
. Например, рассмотрим функцию 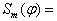
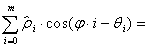
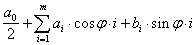 ,
,
РіРґРµ 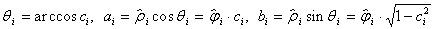 В (
В (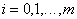 ). Рту функцию можно рассматривать как обобщение дескриптора
Фурье [5]. По функции
). Рту функцию можно рассматривать как обобщение дескриптора
Фурье [5]. По функции   коэффициенты
 коэффициенты   (а, следовательно, и
 (а, следовательно, и 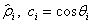 ) будут определяться однозначно, как коэффициенты частичной
суммы ряда Фурье. По дискретным значениям этой функции
) будут определяться однозначно, как коэффициенты частичной
СЃСѓРјРјС‹ СЂСЏРґР° Фурье. РџРѕ дискретным значениям этой функции 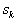 В
  , коэффициенты
, коэффициенты   можно найти из
линейной системы
 можно найти из
линейной системы  ,
,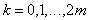 , если значения
, если значения  ,
, 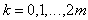 , такие, что определитель матрицы
, такие, что определитель матрицы 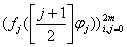  отличен от нуля, где
 отличен от нуля, где  , где
, где  - целая часть числа. Множество функций изображения будем
рассматривать вместе с нормой
- целая часть числа. Множество функций изображения будем
рассматривать вместе с нормой  . Следующая теорема говорит об устойчивости функции
изображения к изменению весов (и, следовательно, к изменению центра масс).
. Следующая теорема говорит об устойчивости функции
изображения к изменению весов (и, следовательно, к изменению центра масс).
Теорема 2. Пусть   и
 и 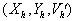  два скелета
изображения
 два скелета
изображения 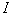  такие, что
 такие, что  . Тогда, если
. Тогда, если 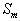 и
и 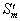  соответствующие этим
скелетам функции изображения, то
 соответствующие этим
скелетам функции изображения, то 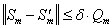 , где
, РіРґРµ  .
.
Однако при добавлении
новой контрольной точки даже с небольшим весом функция изображения, вообще
говоря, может сильно измениться, так как она не является инвариантной
относительно сдвига векторов векторного представления 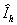 . Таким свойством будет обладать, например, функция
. Таким свойством будет обладать, например, функция 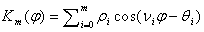 , хотя коэффициенты этой функции уже не будут однозначно
восстанавливаться по ее значениям.
, хотя коэффициенты этой функции уже не будут однозначно
восстанавливаться по ее значениям.
5.Распознавание
симметрий
Рзображение   называется
 называется 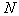 -осесимметричным [6], если оно переводится само в себя после
поворота на любой угол, кратный
-осесимметричным [6], если оно переводится само в себя после
поворота на любой угол, кратный 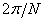  вокруг своего центра
масс. Симметрия является важной в задачах распознавания характеристикой
изображаемого объекта. Подробный обзор существующих методов обнаружения
симметрий и определения ориентации объекта, в том числе и с помощью
дескрипторов Фурье, можно найти в работе [6]. Распознавать симметрию можно
непосредственно анализируя векторное представления
 вокруг своего центра
масс. Симметрия является важной в задачах распознавания характеристикой
изображаемого объекта. Подробный обзор существующих методов обнаружения
симметрий и определения ориентации объекта, в том числе и с помощью
дескрипторов Фурье, можно найти в работе [6]. Распознавать симметрию можно
непосредственно анализируя векторное представления 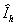 , если оно достаточно точно отражает характер симметрии (не
содержит «лишних» контрольных точек). Векторное представление
, если оно достаточно точно отражает характер симметрии (не
содержит «лишних» контрольных точек). Векторное представление   назовемВ
 назовем 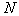 -осесимметричным, если построенный по этому векторному
представлению многоугольник будетВ
-осесимметричным, если построенный по этому векторному
представлению многоугольник будет  -осесимметричным. С другой стороны, для распознавания
симметрии можно использовать и функцию изображения
-осесимметричным. С другой стороны, для распознавания
симметрии можно использовать и функцию изображения 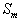 . В этом случае лучше перейти к комплексной форме записи функции
изображения. Обозначим через
. В этом случае лучше перейти к комплексной форме записи функции
изображения. Обозначим через 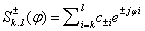 , где
, РіРґРµ 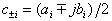 . РўРѕРіРґР°
. Тогда 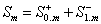  и справедлива
 и справедлива
Теорема 3. 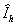  являетсяВ
 является 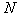 -осесимметричным векторным представлением изображения
-осесимметричным векторным представлением изображения   тогда и только тогда,
когда найдется такое
 тогда и только тогда,
когда найдется такое 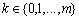 , что
, что  ,
, 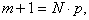 В РіРґРµ
В РіРґРµ .
.
Рто мультипликативное
свойство функции изображения можно использовать для распознавания симметрий, а
именно, если для заданного малого 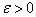  найдутся такие
 найдутся такие 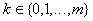  и
 и  , что
, что 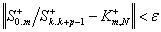 , то можно считать векторное представление
, то можно считать векторное представление  В
  -осесимметричным.
-осесимметричным.
Списоклитературы
Hecker
Y.C., Bolle R.M. On geometric hashing and the generalized Hough transform, IEEE
Trans. Syst., Man and Cybern. 24, N9, 1994, p.1328-1338.
Dufresne
T.E., Dhawan A.P., Chord-tangent transformation for object recognition, Pattern
Recogn. 28, N9, 1995, p.1321-1332.
Bolles
R., Cain R.A., Recognizing and locating partiavisible objects: The
local-feature-focus method, Robot Vision A.Publ. Ed., 1984.
Liu
H.C., Srinath M.D., Partial Shape Classification Using Contour Matching in
Distance Transformer; IEEE Trans. Pattern Anal. and Mach. Intell, 12, N11,
p.1072-1079.
Zahn
C.T., Roskies R.S., Fourier descriptors for plane closed curves, IEEE Trans.
Comput. C-21, March, 1972, p.269-281.
Pei
S.C., Liov L.G., Automatic symmetry determination and normalization for
rotationally symmetric 2D shapes and 3D solid objects, Pattern Recogn, 27, N9,
1994, p.1193-1208. последовательностей".- Таганрог,
РёР·Рґ. РўР РўРЈ, 1996 Рі.




 В В В В В В В В В В В В В В В В В В
В В В В В В В В В В В В В В В В В В 

 , РіРґРµ
, РіРґРµ  .
.