РљСѓСЂСЃРѕРІРѕР№ проект РїРѕ теме «Теоретические РѕСЃРЅРѕРІС‹ информатики» выполнил студент: Лепихов Р.Рњ.
Государственный комитет по образованию Российской Федерации
Московский институт радиотехники, электроники и автоматики, факультет кибернетики, кафедра интеллектуальных технологий и систем
РњРѕСЃРєРІР° 1997
Задание на курсовое проектирование по курсу:
«Теоретические основы информатики»
Студента: Лепихова Р.Рњ. РіСЂ. РР -1-95.
Тема: «Логические схемы в различных функциональных наборах и их реализация»
1. Рсходные данные
1.1. Строка из шестнадцати символов А = { a0,a1, ..., a15 }
Матричный индикатор 5 ґ 7 = 35 ячеек.
Множество признаков H = { h0,h1, ..., h35 }
Условие формирования строки символов и отображения T:H ґ A а F.
Правило выделения ФАЛ из данных пункта 1.3.
Рнтегральный набор Рљ155 (РїРѕ справочнику)
Условие формирования подпространства Ф
Перечень подлежащих разработке вопросов.
2.1. а) отображение Т.
 б) ФАЛ F1, F2, F3.
в) подмножество Ф
Комбинационная схема совместной реализации ФАЛ F1, F2, F3.
Анализ подмножества Ф
Схема автомата, отвечающая состояниям пункта 2.3.
Выводы и заключения.
Тема исследования.
Структура формальной системы отношения по дополнительно заданной предметной области знаний.
Перечень графических материалов.
Отображение T: H ґ A а F.
Комплекс моделей, методов и средств минимизации ФАЛ F1и F2.
Комбинационная схема совместной реализации.
Матрица толерантности, карта толерантности для подмножества Ф
Схема автомата А.
Введение
С развитием электроники приобретают огромное значение электронные визуальные средства отображения информации.
Рти средства представляют СЃРѕР±РѕР№ разнообразной величины экраны, оформленные различными способами (циферблаты часов, табло РЅР° стадионах Рё С‚.Рґ.) РЈ всех этих средств общая деталь - элемент, отображающий только РѕРґРёРЅ СЃРёРјРІРѕР».
Рти элементы представляют СЃРѕР±РѕР№ матрицу, РІ клетках которой смонтированы светящиеся элементы (лампочки Рё С‚.Рї.) РџСЂРё подаче РЅР° РЅРёС… напряжения, отображается тот или РёРЅРѕР№ СЃРёРјРІРѕР» визуальной информации.
Темой данного курсового проекта является разработка автомата, управляющего светящимися элементами, для отображения необходимого сообщения на табло.
Каждый символ сообщения отображается на отдельной матрице (матричном индикаторе) 5 ґ 7 светящихся элементов, то есть каждому символу соответствует определенная комбинация светящихся элементов матрицы.
В данном курсовом проекте нужно выбрать три признака (светящегося элемента) и построить автомат, управляющий этими признаками при подаче на вход четырехразрядного управляющего кода.
Для разработки автомата необходимо произвести анализ на толерантность и эквивалентность. В заключение необходимо сделать вывод.
1. Рсходные данные.
Рсходными данными является строка РёР· шестнадцати символов, Р° так же матричный индикатор, назначение которого будет подробнее рассмотрено РІ пункте 1.2.
1.1. Строка из шестнадцати символов.
Строка из шестнадцати символов выбирается произвольно. Она является объектом исследования. В данном курсовом проекте используется строка, приведенная на рисунке 1.1.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Р | Р’ | Рђ | Рќ | | Рњ | Р | РҐ | Рђ | Р™ | Р› | Рћ | Р’ | Р | Р§ | . |
Рис. 1.1. Строка из шестнадцати символов
1.2. Матричный индикатор.
Матричный индикатор - матрица размерностью 5 ґ 7 = 35 ячеек. С помощью матричного индикатора можно любому символу (букве, знаку препинания, цифре и т.д.) поставить в соответствие набор признаков H = { h1, h2, ..., h35 }. Внешний вид матричного индикатора представлен на рисунке 1.2.

Р РёСЃ. 1.2.
1.3. Формирование отображения строки символов.
С помощью матричного индикатора устанавливается соответствие каждому символу aiиз исходной строки символов А (см. п. 1.1) определенный набор признаков На
устройство должно выдавать сигнал РЅР° соответствующем выходе подтверждающей, что индикатор распознал СЃРёРјРІРѕР» В«РВ». Аналогично должны распознаваться РґСЂСѓРіРёРµ символы строки Рђ, что соответствует отображению T:H Т‘ A, которое представлено РІ таблице 1. РџРѕ горизонтали таблицы расположена строка Рђ символов, РїРѕ вертикали 35 признаков Рќ. Если признак соответствует данной Р±СѓРєРІРµ, то РЅР° пересечении строки-признака Рё столбца-Р±СѓРєРІС‹ ставится В«1В» Рё С‚.Рґ. РґРѕ заполнения всей таблицы. Затем производится подсчет единиц РІ строке.
Для упрощения задачи из всего множества признаков выделяется три признака из 35-ти, для которых строится таблица истинности, причем число единиц для каждого признака подбирается равным 7,8 и 9. Таким образом, устройство классифицирует символы по двум классам объектов: по наличию или отсутствию трех признаков.

| Р РёСЃ. 1.3Р°, отображение символа В«РВ» РЅР° индикаторе | Р РёСЃ. 1.3Р±, РІРёРґ матричного индикатора РїСЂРё изображении символа В«РВ» |
2. Промежуточное исследование исходных данных.
В промежуточном исследовании мы поставим в соответствие буквам строки из 16-ти символов наборы признаков, сформулируем отображение T:H ґ A а F и выделим 3 ФАЛ. Построим для них таблицу истинности и по картам Карно найдем их номера.
2.1. Отображение символов строки А на индикаторе.
С помощью матричного индикатора (см. п.1.2) поставим в соответствие буквам строки из пункта 1.1 наборы признаков (см. рис. 2.1).

Рис. 2.1, отображение символов строки А на индикаторе.
Выпишем отдельно буквы и соответствующие им признаки
Р 1,5,6,10,11,14,15,16,18,20,21,22,25,26,30,31,35
Р’ 1,2,3,4,6,10,11,15,16,17,18,19,21,25,26,30,31,32,33,34
A 2,3,4,6,10,11,15,16,17,18,19,20,21,25,26,30,31,35
H 1,5,6,10,11,15,16,17,18,19,20,21,25,26,30,31,35
пробел
Рњ 1,5,6,7,9,10,11,13,15,16,20,21,25,26,30,31,35
Р 1,5,6,10,11,14,15,16,18,20,21,22,25,26,30,31,35
РҐ 1,5,7,9,12,14,18,22,24,27,29,31,35
A 2,3,4,6,10,11,15,16,17,18,19,20,21,25,26,30,31,35
Р™ 1,3,5,6,10,11,14,15,16,18,20,21,22,25,26,30,31,35
Р› 3,4,5,7,10,11,15,16,20,21,25,26,30,31,35
O 2,3,4,6,10,11,15,16,20,21,25,26,30,32,33,34
Р’ 1,2,3,4,6,10,11,15,16,17,18,19,21,25,26,30,31,32,33,34
Р 1,5,6,10,11,14,15,16,18,20,21,22,25,26,30,31,35
Р§ 1,5,6,10,11,15,16,17,18,19,20,25,30,35
. 35
2.2. Получение ФАЛ
В данном курсовом проекте из множества признаков выделено 3 (см. табл.1). С номерами 1,3,5 для которых и будет построена логическая схема устройства, диагностирующего их наличие или отсутствие.
Для решения задачи в двухзначной логике необходимо перейти к двоичному коду, закодировав им каждый из 16-ти символов строки А.
РџСЂРё этом достаточно четырехразрядного двоичного числа, определяющего значение XYZP, которым РІ дальнейшем будет кодироваться номер каждого символа. Например, второй СЃРёРјРІРѕР» «В» должен иметь РєРѕРґ 0001, первый В«РВ» - 0000 Рё С‚.Рґ.
Таблица истинности для выбранных признаков представлена в таблице 2, где ФАЛ - функция алгебры логики, в которых значение 1 принимается для кодов, имеющих значение признака h, равного 1. В общем случае h М {0,1}. Следует учесть, что h1аF1, h3аF3, h5аF5.
Отображение T:H ґ A а F

Табл. 1
2.3. Нахождение номеров ФАЛ по карте Карно
Следующим этапом является нахождение 10-значных номеров ФАЛ по карте Карно, общий вид которой для 4-ех переменных представлен на рисунке 2.2. Цифры в квадратах являются степенью числа 2 при определении номера ФАЛ, выбранных в данной работе на рисунке 2.2а,б,в

Рис. 2.2 Карта Карно со степенями двойки
2.4. Таблица истинности.

Табл. истинности для ФАЛ. Табл. 2
Нахождение номера ФАЛ: F1
| 
| N(F1) = 20 + 21 + 23 + 25+ 27 + 26 + 29 + 212 + + 213 + 214 = 29419 |
Нахождение номера ФАЛ: F3
| 
| N(F3) = 21 + 22 + 212 + 28+ 29 + 210 + 211 = 7942 |
Нахождение номера ФАЛ: F5
| 
| N(F5) = 20 + 23 + 25 + 26 + 27 + 29+ 210 + 213 + + 214 = 26345 |
2.5. Представление ФАЛ в совершенной нормальной форме.
Представим выбранные признаки в совершенной дизъюнктивной нормальной форме (СДНФ) и совершенной конъюнктивной нормальной форме (СКНФ). Для этого из таблицы истинности ФАЛ (см. табл. 2) выпишем конституэнты 0 и 1.
ФАЛ в СДНФ примет вид:
F1(X,Y,Z,P) = (X,Y,Z,P) РЄ (X,Y,Z,P) РЄ (X,Y,Z,P) РЄ (X,Y,Z,P) РЄ
(X,Y,Z,P) РЄ (X,Y,Z,P) РЄ (X,Y,Z,P) РЄ (X,Y,Z,P) РЄ (X,Y,Z,P) РЄ (X,Y,Z,P)
F3(X,Y,Z,P) = (X,Y,Z,P) РЄ (X,Y,Z,P) РЄ (X,Y,Z,P) РЄ (X,Y,Z,P) РЄ
(X,Y,Z,P) РЄ (X,Y,Z,P) РЄ(X,Y,Z,P)
F5(X,Y,Z,P) = (X,Y,Z,P) РЄ (X,Y,Z,P) РЄ(X,Y,Z,P) РЄ (X,Y,Z,P) РЄ
(X,Y,Z,P) РЄ (X,Y,Z,P) РЄ(X,Y,Z,P) РЄ (X,Y,Z,P) РЄ (X,Y,Z,P)
ФАЛ в СКНФ примет вид:
F1(X,Y,Z,P) = (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P)
F3(X,Y,Z,P) = (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P)
F5(X,Y,Z,P) = (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P) & (X РЄ Y РЄ Z РЄ P)
2.6. Минимизация ФАЛ
Проведем минимизацию полученных ФАЛ при помощи карты Карно и представим их в ДНФ. Для этого попытаемся оптимальным образом объединить 0-кубы в кубы большей размерности. Клетки, образующие k-куб, дают минитерм n-k ранга, где n - число переменных, которые сохраняют одинаковое значение на этом k-кубе. Таким образом, получим ДНФ выбранных ФАЛ.

Р РёСЃ 2.2Р° Р РёСЃ 2.2Р± Р РёСЃ 2.2РІ
Проведем минимизацию алгебраическим путем, воспользовавшись тождеством а Ра = а.
XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP = XYZ РЄ XZP РЄ XZP РЄ YZP РЄ XYZ РЄ XZP = ZP РЄ XYZ РЄ XZP РЄ YZP РЄ XYZ
XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZPРЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP = YZP РЄ YZP РЄ XZP РЄ XYZ РЄ XYZ = XY РЄ YZP РЄ YZP РЄ XZP
РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZPРЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP РЄ XYZP = XZP РЄ XYP РЄ XYZ РЄ XZP РЄ XZP РЄ XYZP
2.7. Представление ФАЛ в виде куба
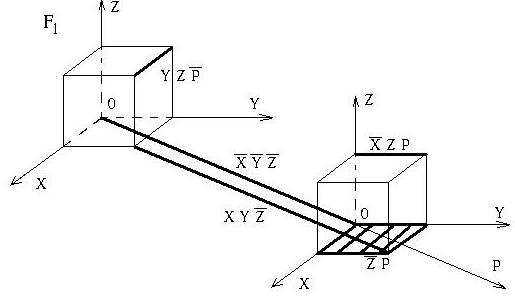


3. Рсследование ФАЛ.
3.1. Матрица отношений.
Построить матрицу отношений T:H ґ A. Матрица отношений представляет собой таблицу, строками которой являются записи (кортежи признаков), а строками отношения, которые имеют все уникальные имена. Матрица отношения представлена в таблице 3.

Матрица отношений. Табл. 3
3.2. Рсследование ФАЛ РЅР° толерантность.
Определим классы толерантности. Рассмотрим классы толерантности k1, k2, k3, имеющие общие элементы, следовательно, являющиеся пересекающимися множествами.
h1 = h(a1) = h(A) = { X0, X1, X3, X5, X6, X7, X9, X12, X13, X14 }
h2 = h(a2) = h(B) = { X1, X2, X8, X9, X10, X11, X12 }
h3 = h(a3) = h(C) = { X0, X3, X5, X6, X7, X9, X10, X13, X14 }
Проанализировав классы h1, h2, h3, можно получить: k1 З k2 = 0;
k1 З k3 = 0; k2 З k3 = 0, т.е. {k1, k2, k3 } - образуют класс толерантности
Результаты исследования занесем в таблицу 3.
3.3. Рсследование ФАЛ РЅР° эквивалентность.
Определим классы эквивалентности для этого множества А = {Х0, Х1, ...., Х15 } разобьем на классы эквивалентности, получим 6 классов
Рњ1= {AC} = {X0,X3,X5,X6 X7,X13,X14}
Рњ2= {AB} = {X1,X12}
Рњ3= {B} = {X2,X8,X11}
Рњ4= { } = {X4,X15}
Рњ5= {ABC} = {X9}
Рњ6= {BC} = {X10}
При этом каждый класс полностью определяется любым его представителем. Сопоставив результаты исследования с результатами пункта 3.2 получим следующие зависимости
| Рњ1 Рњ K1 | Рњ2 Рњ K1 | Рњ3 Рњ K2 | Рњ5 Рњ K1 | Рњ6 Рњ K2 |
| Рњ1 Рњ K3 | Рњ2 Рњ K2 | | Рњ5 Рњ K2 | Рњ6 Рњ K3 |
| | | | Рњ5 Рњ K3 | |
или
K1 = M1 Р M2 Р M5
K2 = M2 Р M3 Р M5Р M6
K3 = M1 Р M5 Р M6
Результаты исследования занесены в таблицу 3. Результаты исследования на эквивалентность и толерантность необходимы для оптимизации построения логической схемы.
3.4. Матрица эквивалентности и толерантности.
Матрицу эквивалентности и толерантности можно представить в виде квадрата, по диагонали которого строятся классы эквивалентности, а затем устраиваются отношения толерантности. Матрица эквивалентности и толерантности представлена в таблице 4.
Матрица эквивалентности и толерантности. Таблица 4.
3.5. Диаграмма Рйлера.
Диаграмма Рйлера дает наглядное представление Рѕ том, как распределяются признаки РїРѕ классам толерантности Рё эквивалентности. Диаграмма Рйлера для выбранных ФАЛ представлена РЅР° СЂРёСЃСѓРЅРєРµ 3.5.

Диаграмма Рйлера. Р РёСЃ. 3.5
3.6. Построение комбинационной схемы.
Комбинационная схема автомата распознавания набора признаков H = {h1, h3, h5 } построена на основе результатов исследований в пункте 3.1 и пункте 3.4.

Таблица 5
Рспользуя таблицу 5, можно записать следующие отношения:
G1= (XYZP) РЄ (XYZP) РЄ (XYZP) РЄ (XYZP) РЄ (XYZP) РЄ (XYZP) РЄ (XYZP) = (XYZP) РЄ (XYZP) РЄ (XYZP) РЄ (XYZ) РЄ (YZP)
G2= (XYZP) РЄ (XYZP)
G3= (XYZP) РЄ (XYZP) РЄ (XYZP)
G4= (XYZP) РЄ (XYZP)
G5= (XYZP)
G6= (XYZP)
Тогда ФАЛ можно представить в виде:
F1 = G1 РЄ G2 РЄ G5
F3 = G2 РЄ G3 РЄ G5РЄ G6
F5 = G1 РЄ G5 РЄ G6
Рти отношения эквивалентны ФАЛ РІ СДНФ, полученным РІ пункте 2.5.
Комбинационная схема строилась в два этапа:
1 этап: - построение комбинационной схемы на элементах и, или,
(нестандартных).
2 этап: - замена нестандартных элементов на стандартные и-не
Заключение
Проведя анализ на толерантность и эквивалентность, мы построили автомат, распознающий кортеж признаков H = {h1, h3, h5 }, который состоит из 16 - ти логических элементов.
Список литературы
1. В.П. Сигорский. «Математический аппарат инженера» - издательство Киев: Техника - 1975 г.


















